Qu’est-ce que l’ICM au Poker ? (et le calculer simplement)
Au poker, l’Independent Chip Model (ICM) est un modèle mathématique utilisé pour calculer l’équité globale d’un joueur dans un tournoi. Le modèle utilise uniquement la taille des piles pour déterminer combien de fois un joueur finira dans chaque position (1er, 2e, etc.)
Définition de l’ICM au Poker

Au poker, l’ICM vous permet de convertir les piles de jetons des joueurs de tournois en leur valeur monétaire (en pourcentage du total ou de la cagnotte restante).
L’ICM peut être utilisé pour réaliser des coups justes sur la table finale d’un tournoi de poker à plusieurs tables ou pour comparer les valeurs monétaires de différentes décisions prises au cours d’une partie.
En substance, l’ICM au poker est la fonction de seulement deux paramètres d’entrée : une liste des paiements et une liste des piles de jetons dans le tournoi, et il ignore des choses comme les avantages des compétences, la position et la taille des blindes.
L’ICM utilise ces informations de la liste des paiements et de la liste des piles de jetons pour produire une liste des valeurs en euros correspondantes pour chaque pile, qui sont représentatives de leur part dans la cagnotte restante.
L’équité ICM du poker peut être facile à comprendre dans le contexte d’un coup de table final – elle permettrait à chaque joueur de déterminer quelle part de la cagnotte va dans sa poche si le tournoi s’était terminé à ce moment sans autre jeu, et ce montant devrait être le même, en moyenne, si le tournoi se déroulait jusqu’à la fin.
Il existe différents modèles de ICM au poker qui se distinguent les uns des autres par leur approche du calcul des probabilités que chaque pile se termine à chaque position potentielle.
Le modèle de l’ICM au poker le plus populaire et le plus éprouvé est le modèle de Malmuth-Harville.
Pourquoi utilisons-nous l’ICM dans les tournois de poker ?
Lorsque vous jouez à un jeu d’argent, la valeur de vos jetons est constante, ils représentent un euro.
Ainsi, chaque jeton vaut exactement un euro, et votre objectif est simplement d’en obtenir le plus grand nombre possible. Mais quand vous jouez dans un tournoi, les choses ne sont pas si simples.
Prenons un exemple simple :
3 joueurs entrent dans un tournoi avec un buy-in de 100€ (en ignorant le rake), ils obtiennent chacun 100 jetons à 5/10 blindes, et jouent pour une cagnotte de 300€ divisés en 195€ pour la 1ère place, 105€ pour la 2ème, et 0€ pour la 3ème.
Dans la première main, le joueur 1 se couche, le joueur 2 fait tapis, le joueur 3 suit, perd la main et est éliminé du tournoi.
Avant le jeu, chaque joueur a payé 100 € pour ses 100 jetons, et toutes choses étant égales par ailleurs, a évidemment une chance égale d’arriver à l’une des 3 positions. Vous pourriez penser que ces 100 jetons valent 100 € et que, selon cette logique, chaque jeton vaut 1 € mais réfléchissons à ce qui s’est passé ici.
Le joueur 3 a perdu ses 100 jetons et les 100 € qu’il avait l’habitude d’acheter, et le joueur 2 a doublé sa pile de départ, mais a-t-il doublé son équité dans le tournoi ? Non.
Le joueur 2 s’est assuré une deuxième place, et les 105 € qui l’accompagnent, et s’est donné une avance de 2:1 en jetons, s’imposant comme le favori pour gagner le match.
Mais remarquez que même s’il gagne tout le tournoi, il n’aurait même pas doublé son capital de 100 €, car la première place ne rapporte que 195 € et il n’est toujours pas garanti de gagner.
Qu’est-il donc arrivé au capital restant ? Il est allé au joueur 1, qui n’avait pas gagné ou perdu un seul jeton, mais qui avait augmenté son capital de départ de 100 € pour se retrouver dans une situation où il a bloqué un prix minimum de 105 € pour le deuxième et dispose d’un capital au moins un peu plus élevé que cela puisqu’il a encore une chance de jouer pour le premier.
La valeur des jetons de tournoi n’est donc pas constante, elle est liée à votre capacité à utiliser ces jetons pour gagner de l’argent en terminant dans les places payantes.
Et cela dépend de nombreux facteurs tels que
- votre compétence relative sur le terrain,
- les gains,
- le nombre de joueurs,
- la taille de leur pile,
- leur position, …, et ainsi de suite.
C’est vraiment assez complexe, et il n’est pas possible de tenir compte de tous les facteurs en jeu pour prendre les meilleures décisions, donc nous avons besoin d’un moyen d’approximer la valeur de nos jetons et des jetons ajoutés et pris dans notre pile – c’est exactement ce que fait ICM, et il le fait bien.
En fait, il le fait si bien que pratiquement tous les grands gagnants des MTT et des Sit-and-Go l’utilisent pour guider leur jeu dans les situations critiques.
Il s’est avéré être le modèle le plus précis à maintes reprises, et dans un domaine compétitif où des millions d’euros sont en jeu, c’est énorme !
Les effets du facteur de bulle, du facteur ICM et les effets variables de la pression ICM

L’effet restrictif que les considérations d’équité des tournois ont sur l’éventail des mains jouables d’un joueur est communément appelé “pression ICM”.
Lorsque le risque de perdre des fonds propres supérieurs à la moyenne devient plus important, et que le jeu correct impose de jouer des plages plus étroites par rapport au poker (comme le cash game), on dit qu’un joueur est soumis à une “forte pression ICM”.
Lorsque ce risque est plus faible et que les marges de jeu se rapprochent du jeton, le joueur est considéré comme étant soumis à une “faible pression ICM”.
La pression peut être mesurée par la distance entre les cotes nécessaires pour qu’un jeu présente une valeur positive en jetons et les cotes nécessaires pour qu’un jeu présente une valeur positive en € ou en équité ICM (valeur monétaire réelle).
Cette distance est appelée “Facteur de Bulle” ou “Facteur ICM” et peut être utilisée pour déterminer la gamme de mains qui peuvent être jouées avec profit en déterminant si elles satisfont aux exigences de cotes du Facteur ICM par rapport à la gamme de l’adversaire.
Utiliser l’ICM pour concevoir des stratégies optimales
Maintenant que nous savons ce que fait l’ICM nous pouvons commencer à l’utiliser pour planifier nos stratégies dans les tournois.
Pour ce faire, nous utilisons la conversion de l’équité ICM pour comparer la différence de valeur attendue de notre pile entre nos options de se coucher ou de jouer (de toutes les manières possibles) les mains qui nous sont distribuées.
- Tournoi : 6max
- Paiements : 1er – 65 €, 2e – 35 €, 3e – 0
- Blindes : 100/200
- BTN : 4 000, PB : 3 000, GB : 2 000
- Preflop : Grosse blinde s’occupe de KQo
- Bouton pousse le all-in, Petite Blinde se couche, action sur la Grosse Blinde
et supposons que la grosse blinde a de bonnes raisons de croire que le Bouton pousse la gamme suivante
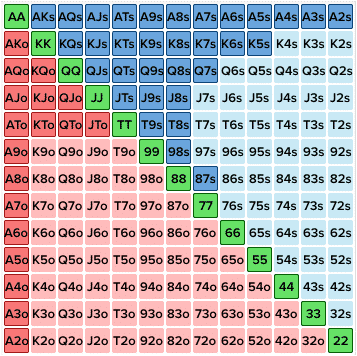
{22+,A2+,K5s+,KTo+,Q7s+,QTo+,J8s+,JTo,T8s+,98s,87s}
En utilisant un calculateur d’équité de base, nous pouvons voir que, par rapport à la plage de poussée de ce bouton, le KQo du la grosse blinde gagnera 46,74 % du temps, sera à égalité 3,53 % du temps et perdra 49,73 % du temps lorsqu’il appellera le all-in.
Une petite remarque – S’il s’agissait d’une main de cash game, nous regarderions simplement nos chances d’appeler 1 800 jetons dans un pot de 2 300 pour voir que nous avons besoin de 43,9 % de fonds propres pour faire un appel rentable, et en étant clairement au-dessus de ce chiffre, nous pouvons voir que c’est un appel +chipEV, mais le poker de tournoi n’est pas aussi facile à résoudre.
Ainsi, 46,74 % des piles de fin seront [BTN : 2 000, PB : 2 900, GB : 4 100] et 3,53 % des fois où GB et BTN sont à égalité pour couper le poteau la petite blinde, ils seront [BTN : 4 050, PB : 2 900, GB : 2 050]. Les 49,73% du temps où BB perd le montant total de ses €EV seront évidemment de 0 €.
Nous pouvons insérer toutes ces configurations de fin de pile dans notre calculateur ICM de poker pour voir l’ICM_€EV de chaque résultat, multiplier ces EV par leur probabilité de se produire, et additionner ces chiffres pour obtenir notre EV ICM global de la poussée.
| EV (% prime) | Probabilité | |
| Gagner | 41.75 | 46.74 |
| Egalité | 25.12 | 3.53 |
| Perdre | 0 | 49.73 |
En multipliant les EV de chaque pile finale par sa probabilité d’occurrence et en additionnant ces chiffres, nous pouvons voir que l’EV globale de la poussée avec KQo est
(0,4175 * 0,4674) + (0,2512 * 0,0353) + (0,0 * 0,4973) = 0,20400686 = 20,40 EV
Maintenant que nous connaissons la valeur de la stratégie de KQo, nous avons besoin d’une dernière information pour déterminer quelle est notre action la plus rentable – vous souvenez-vous de cette information ? Prenez un moment pour y réfléchir avant de poursuivre votre lecture.
La dernière information cruciale dont nous devons tenir compte est la valeur attendue de notre fold. Sans connaître l’EV du fold, nous n’aurions rien à comparer à l’EV de la poussée.
Nous noterons que si la GB se couche au coup du Bouton, elle perd sa position de 200 jetons et nous avons une pile de fin de [BTN : 4,300, PB : 2,900, GB : 1800] et ICM nous dit que cette configuration donne au joueur de GB un EV de (EV Fold : 22.73%) et nous pouvons comparer cela à (EV Call : 20.40%) pour voir que GB devrait clairement préférer se coucher comme cela vaut (22.73 – 20. 40) = 2,33% de la cagnotte de plus que l’appel, et pour un joueur moins expérimenté 2,33% peut sembler peu mais en réalité c’est une somme absolument énorme d’équité – représentant plus d’argent en une seule décision que les plus grands gagnants des SnG de 1 table font en moyenne dans un jeu entier – assurons-nous de choisir le bon côté de cette décision aussi souvent que possible.
Si les calculs précédents ne semblent pas triviaux, cela peut indiquer que la meilleure option est d’utiliser une calculatrice de poker.
Dans les jeux d’argent, ce calcul de comparaison de l’EV d’une main à l’EV d’une main couchée est si trivial qu’il est facile d’oublier que nous le faisons tout court – lorsqu’un joueur de jeux d’argent est hors des blindes, il doit juste surpasser son 0 € de couchée, et lorsqu’il est dans les blindes, il doit surpasser la perte de sa blinde affichée lorsqu’il se couche.
Mais, une fois de plus, nous constatons que les choses ne sont pas si faciles dans les tournois de poker.
Défauts de l’ICM au poker

L’ICM est un modèle merveilleux, mais il n’est pas parfait.
Avant de conclure cet article, parlons des lacunes du modèle ICM au poker.
L’ICM suppose que le jeu se termine maintenant.
Pour déterminer les véritables VE d’un jeu dans un tournoi de poker, il faudrait savoir comment chaque main possible dans le tournoi, à partir de ce point jusqu’à chaque conclusion possible, se jouerait pour tous les joueurs restants.
Il est clair que c’est beaucoup trop complexe pour qu’il y ait le moindre espoir de modélisation dans des situations autres que les plus incroyablement élémentaires, c’est pourquoi nous nous tournons vers des modèles qui simplifient le jeu et c’est exactement ce que fait l’ICM.
En tant que modèle, l’ICM simplifie le jeu réel, d’une complexité impossible, en un jeu beaucoup plus simple, où tout s’arrête et où chaque joueur est simplement payé, dès maintenant, sa part de la cagnotte du tournoi, entièrement basée sur sa taille de pile et celle de chaque autre joueur.
L’ICM ignore des éléments importants comme l’adresse, la position, les blindes ou tout autre jeu de poker réellement joué.
Ainsi, ICM ne considère pas que le joueur UTG va placer un gros blind à la prochaine main, ou que les blinds vont augmenter dans les 2 mains – en fait, ICM ne sait même pas qu’il y a des blindes dans ce jeu !
ICM ne sait pas que le joueur du siège 2 est en train de basculer, que le joueur du siège 5 est assis, ou que vous êtes, de toute évidence, le meilleur joueur au monde sur une table pleine d’ânes et de poissons.
L’ICM nous donne simplement un modèle pour estimer la valeur d’une pile de jetons, et nous utilisons ensuite ces valeurs estimées pour comparer les différents jeux parmi lesquels nous pouvons choisir en modélisant une main réelle de poker, en tenant compte des blindes et de l’habileté (fourchettes choisies) pour cette seule main.
Mais à la fin de ce modèle pour cette seule main, une fois de plus, l’ICM suppose que tout s’arrête et que tous les joueurs reçoivent immédiatement leur part de la cagnotte de l’ICM, et toutes les informations qui existent dans le monde réel (compétence, rotation et augmentation des blindes, etc.) sont ignorées.
Pourquoi devriez-vous faire partie des calculateurs ICM ?
Connaître la valeur de vos jetons aux différentes étapes d’un tournoi est un grand pas en avant. Disons que vous êtes assis dans un tournoi de poker, que vous avez une pile confortable et que la bulle approche.
N’aimeriez-vous pas savoir combien d’argent vous pouvez espérer gagner à long terme ?
Que diriez-vous de doubler la mise ? Cela vaut-il la peine de mettre en péril votre pile saine juste avant la bulle ? Et combien cela vous coûterait-il de perdre la moitié de votre pile ?
La structure spécifique des paiements des tournois de poker rend toutes ces questions assez délicates. Des jetons deux fois plus nombreux ne valent pas toujours deux fois plus.
Parfois, il est beaucoup plus important de survivre à la bulle (ou au prochain saut de paiement) que d’accumuler plus de jetons.
Le simple fait de compter vos jetons vous aidera rarement à évaluer exactement votre situation dans un tournoi.
Quelle est la valeur d’un jeton dans un tournoi de poker ?
Prenons un exemple très simple. Supposons que vous jouez à un sit-and-go :
- Buy-in : 10
- Nombre de joueurs : 10
- Paiements : 1er – 50 €, 2e – 30 €, 3e – 20
Pile initiale : 1 000 jetons
Dès le début de ce tournoi, 1 000 jetons valent évidemment 10 euros. Mais au fur et à mesure que le tournoi avance, leur valeur va changer radicalement.
Supposons que vous arriviez à peine à gagner de l’argent, et qu’après que sept joueurs se soient arrêtés, il vous reste 1 000 jetons.
Maintenant, vous êtes assuré d’avoir au moins l’argent de la troisième place. Vos 1 000 jetons valent donc au moins 20 euros.
Même si vous avez réussi à gagner de l’argent avec un seul jeton, ce jeton vaut au moins 20 €.
La valeur des jetons peut augmenter énormément pendant un tournoi.
Mais leur valeur peut aussi diminuer. Supposons que vous réussissiez à gagner le sit-and-go.
Vous aurez alors les 10 000 jetons, mais vous ne recevrez que 50 €. Ainsi, 1 000 de vos jetons ne valent plus que 5 €.
La communauté du poker a mis au point le modèle de jetons indépendants pour attribuer une valeur monétaire précise au nombre de jetons.
Tous les joueurs professionnels de tournois connaissent ce modèle et vous devriez vous aussi.
Comment fonctionne l’ICM au poker ?
L’Independent Chip Model condense les deux choses suivantes en une seule valeur pour chaque joueur :
La structure de paiement
La taille des piles de tous les joueurs restants
mathématiques de l’icm au poker
De nombreux esprits brillants ont essayé la formule magique.
En se basant sur la taille des piles, l’ICM calcule pour chaque joueur la probabilité de finir 1er, 2ème, etc. et multiplie ces probabilités par les gains pour chaque position.
Pour calculer la probabilité qu’un certain joueur finisse premier, il suffit de diviser le nombre de ses jetons par le nombre total de jetons en jeu. Les probabilités de terminer 2e ou moins sont calculées de manière similaire mais légèrement plus complexe.
Les calculs sont en fait si complexes que vous avez généralement besoin d’un ordinateur. Pour 4 joueurs, il faut passer par plus de 20 étapes de calcul. Pour 10 joueurs, vous avez déjà besoin de millions.
Heureusement, de nombreux calculateurs ICM décents sont disponibles gratuitement en ligne. Voici un exemple.
Un exemple de calcul facile de l’ICM
Revenons à notre précédent exemple de sit-and-go :
- Buy-in : 10
- Nombre de joueurs : 10
- Paiements : 1er – 50 €, 2e – 30 €, 3e – 20
- Pile initiale : 1 000 jetons
Supposons maintenant qu’après un certain temps, il ne reste plus que 4 joueurs et que ce sont leurs tailles de pile :
- Joueur 1 : 1 000 jetons
- Joueur 2 : 2 000 jetons
- Joueur 3 : 2 000 jetons
- Joueur 4 : 1 000 jetons
Quelle est la valeur de ces jetons ? Il suffit d’entrer la taille des piles et les paiements dans un calculateur ICM et vous obtiendrez les résultats suivants :
Joueur 1 : 5 000 jetons ≅ 37,18
Joueur 2 : 2 000 jetons ≅ 24,33
Joueur 3 : 2 000 jetons ≅ 24,33
Joueur 4 : 1 000 jetons ≅ 14,17
Si nous supposons que tous les joueurs sont également qualifiés, ils peuvent s’attendre à gagner autant à long terme.
Le joueur 1, qui détient 50 % de tous les jetons, gagnera beaucoup plus que l’argent de la deuxième place. Les joueurs 2 et 3 peuvent s’attendre à gagner un peu plus que l’argent de la troisième place. Même le joueur 4, qui a une pile courte, peut s’attendre à gagner un peu d’argent.
Comment prendre de bonnes décisions basées sur l’ICM
Nous savons maintenant ce que valent les jetons à long terme, mais comment ces connaissances nous aident-elles à prendre de meilleures décisions à l’heure actuelle ?
Revenons à notre exemple et, par souci de simplicité, supposons qu’il n’y a pas de blinde ou de mise en jeu et que vous êtes le joueur 3. La situation suivante se présente :
- Joueur 1 (BU) : 1 000 jetons
- Joueur 2 (PB) : 2 000 jetons
- Joueur 3, vous (GB) : 2 000 jetons
- Joueur 4 (UTG) : 1 000 jetons
Le joueur 4 et le joueur 1 se couchent tous les deux et le joueur 2 fait tapis pour 2 000 jetons. Vous tenez un As neuf (non adapté) et … ?
Devriez-vous suivre ou vous coucher ?
Supposons en outre que vous connaissez assez bien le joueur 2 car vous jouez très souvent contre lui et vous savez qu’il bluffe assez souvent dans ces situations. Dans l’ensemble, vous supposez que vous gagnerez l’épreuve de force six fois sur dix si vous appelez son all-in.
Vous êtes donc le favori si vous appelez, mais dans les tournois, il ne suffit parfois pas d’être simplement le favori. Analysons la situation en utilisant l’ICM. Trois choses peuvent se produire après que le joueur 2 ait fait tapis :
- Vous vous couchez (la taille des piles reste la même)
- Vous appelez et vous gagnez (vous avez maintenant 4 000 jetons et le joueur 2 est grillé)
- Vous appelez et vous perdez (vous êtes maintenant grillé et le joueur 2 a 4 000 jetons)
Pour les trois situations, nous pouvons maintenant calculer les valeurs ICM :
| Piles après le fold | ICM-EV | Les piles après l’appel et la victoire | ICM-EV | Piles après appel et perte | ICM-EV | |
| Joueur 1 | 5 000 | 37.18 € | 5 000 | 38.89 € | 5 000 | 38.89€ |
| Joueur 2 | 2 000 | 24.33 € | 0 | 0 € | 4 000 | 36.44€ |
| Joueur 3 (vous) | 2 000 | 24.33 € | 4 000 | 36.44 € | 0 | 0€ |
| Joueur 4 | 1 000 | 14.17 € | 1 000 | 24.67 € | 1 000 | 24.67 € |
Cela signifie que si vous appelez et gagnez, vous aurez 4 000 jetons et ces jetons vous rapporteront 36,44 € à long terme. Mais si vous appelez et perdez, vous n’aurez aucun jeton et vous n’aurez rien à gagner sur le long terme.
Nous avons déjà établi que vous gagnez l’épreuve de force 60 % du temps. Nous pouvons donc facilement calculer votre valeur attendue (EV) pour les appels :
EV = 60% * 36.44€ + 40% * 0€ = 21.86€
En moyenne, vous pouvez vous attendre à gagner 21,86 € si vous appelez le all-in. Comparons maintenant ce chiffre à la valeur attendue si vous vous couchez simplement : 24,33 € – c’est plus de 2 € de plus !
Cela signifie que dans cet exemple, l’ICM conseille un fold comme le meilleur jeu à long terme bien que vous soyez un favori à 60% pour gagner la main ! Mais pourquoi le fold est-il la meilleure option ?
Tout simplement parce que le joueur 4, la pile courte, vous oblige à vous coucher alors qu’il n’est même pas impliqué dans la main.
Il vaut mieux que vous attendiez qu’il se couche plutôt que de mettre tous vos jetons en jeu.
Si vous attendez patiemment, il fera probablement faillite avant vous et vous aurez l’argent de la troisième place garanti. Mais si vous faites appel au forfait, il y a de fortes chances pour que vous vous fassiez arrêter le premier.
L’ICM tient compte de ces considérations et vous conseille correctement de vous coucher.
Qu’en pensez vous ?
Vous êtes libre de laisser un commentaire ci-dessous
Que signifie ICM au poker ?
Independent Chip Model (ICM)
Au poker, l’Independent Chip Model (ICM) est un modèle mathématique utilisé pour calculer l’équité globale d’un joueur dans un tournoi. Le modèle utilise uniquement la taille des piles pour déterminer combien de fois un joueur finira dans chaque position (1er, 2e, etc.).
Comment l'ICM est-il calculé au poker ?
Sur la base de la taille des piles, l’ICM calcule pour chaque joueur la probabilité de finir 1er, 2ème, etc. et multiplie ces probabilités par les gains pour chaque position. Pour calculer la probabilité qu’un certain joueur finisse premier, il suffit de diviser le nombre de ses jetons par le nombre total de jetons en jeu.
Qu'est-ce que la pression ICM ?
L’effet restrictif que les considérations d’équité des tournois ont sur l’éventail des mains jouables d’un joueur est communément appelé “pression ICM”.
Qu'est-ce que l'EV au poker ?
Expected value – communément appelée EV – est le résultat à long terme de vos décisions dans une main de poker particulière


