Compter les Points et les Probabilités au Poker
Dans notre leçon de mathématiques et de probabilités au poker, il a été dit que lorsqu’il s’agit de poker, “les mathématiques sont essentielles“.
Bien qu’il ne soit pas nécessaire d’être un génie des mathématiques pour jouer au poker, une bonne compréhension des probabilités vous sera utile et connaître les probabilités est ce qui compte au poker.
Il a également été dit qu’au poker, il y a de bonnes et de mauvaises mises.
Le jeu détermine simplement qui peut faire la différence.
Cette affirmation est liée à l’importance de connaître et de comprendre les mathématiques du jeu.
Dans cette leçon, nous allons nous concentrer sur les probabilités au poker et sur la façon de calculer vos chances d’obtenir une main gagnante.
Nous débuterons par quelques mathématiques de base avant de vous montrer comment calculer correctement vos probabilités.
Ne vous inquiétez pas pour les maths complexes; nous vous montrerons comment faire des calculs, mais nous vous proposerons également quelques raccourcis simples et faciles à mémoriser.
Mathématiques de base – probabilités et pourcentages

Les probabilités peuvent être indiquées à la fois “pour” et “contre”.
Utilisons un exemple de poker pour illustrer ce point.
Les chances de ne pas tirer une couleur lorsque vous détenez quatre cartes de la même couleur et qu’une carte est à venir s’expriment approximativement à 4 contre 1.
Il s’agit d’un rapport, et non d’une fraction. Cela ne signifie pas “un quart”.
Pour calculer les probabilités pour cet événement, il suffit d’additionner 4 et 1, ce qui donne 5.
Dans cet exemple, vous devriez donc vous attendre à toucher votre couleur 1 fois sur 5.
En termes de pourcentage, cela s’exprimerait en 20% (100 / 5)
Voici quelques exemples :
- 2 pour 1 contre = 1 fois sur 3 = 33,3%.
- 3 pour 1 contre = 1 fois sur 4 = 25%
- 4 pour 1 contre = 1 fois sur 5 = 20%
- 5 pour 1 contre = 1 fois sur 6 = 16,6%.
Conversion des probabilités en pourcentage :
- 3 contre 1 : 3 + 1 = 4. Puis 100 / 4 = 25 %.
- Probabilités de 4 contre 1 : 4 + 1 = 5. Puis 100 / 5 = 20%.
Conversion d’un pourcentage en probabilités:
- 25% : 100 / 25 = 4. Puis 4 – 1 = 3, ce qui donne une cote de 3 pour 1.
- 20% : 100 / 20 = 5. Puis 5 – 1 = 4, ce qui donne une cote de 4 contre 1.
Une autre méthode de conversion du pourcentage en probabilités consiste à diviser le pourcentage de chance lorsque vous ne touchez pas par le pourcentage que vous touchez.
Par exemple, avec 20 % de chances de toucher (comme dans un tirage au sort), nous ferions la chose suivante : 80 % / 20 % = 4, donc 4 pour 1.
Voici quelques autres exemples :
- 25 % de chances = 75 / 25 = 3 (donc, 3 chances sur 1).
- 30 % de chances = 70 / 30 = 2,33 (donc, 2,33 contre 1).
Certaines personnes sont plus à l’aise pour travailler avec des pourcentages plutôt qu’avec des probabilités, et vice versa.
L’essentiel est que vous compreniez clairement comment fonctionnent les probabilités, car nous allons maintenant utiliser cette connaissance des probabilités dans le jeu de poker.
Comptez vos probabilités

Avant de pouvoir commencer à calculer vos probabilités au poker, vous devez connaître vos “outs”.
Par exemple, si vous êtes sur un tirage au sort avec quatre coeurs dans votre main, alors il y aura neuf coeurs (out) restant dans le jeu pour vous donner une couleur.
N’oubliez pas qu’il y a treize cartes dans une couleur, ce qui est facile à calculer ; 13 – 4 = 9.
Un autre exemple serait si vous teniez une main comme 7♣ 6♣ et frappiez deux paires sur le flop de 6♠ 7♦ A♥.
Vous avez peut-être déjà la meilleure main, mais il y a place à l’amélioration et vous avez quatre façons de faire un full.
L’une des cartes suivantes vous aidera à améliorer votre main pour obtenir un full ; 7♠ 7♥ 6♥ 6♦.
Le tableau suivant fournit une courte liste de quelques sorties courantes pour le jeu post-flop. Je vous recommande de retenir ces sorties :
Tableau n°1 – Des probabilités pour améliorer votre main
| Probabilités | Votre prise | Espoir à faire |
| 2 | Une paire | Trois d’entre eux |
| 4 | Deux paire | Poker complet |
| 4 | Quinte intérieur | Quinte |
| 8 | Quinte illimité | Quinte |
| 9 | Quatre couleur | Couleur |
| 15 | Quinte / Tirage de couleur | Quinte / Couleur + |
Le tableau suivant fournit une liste d’autres types de tirages et donne des exemples, y compris les probabilités spécifiques nécessaires pour faire votre main.
Prenez un moment pour examiner ces exemples :
Tableau n° 2 – Exemples de tirage
| Type de tirage | Main | Les Flop | Des Probabilités spécifiques | Probabilités |
| Une paire servie à miser | 2♦ – 2♣ | D♦ – 4♥ – 9♠ | 2♥ – 2♠ | 2 |
| Carte supérieure au tableau | A♠ – 8♦ | V♣ – 5♠ – 2♦ | A♣ – A♦ – A♥ | 3 |
| Tirage de quinte à l’intérieur | V♥ – 9♣ | D♠ – 8♦ – 4♣ | 10♠ – 10♥ – 10♣ – 10♦ | 4 |
| Deux paires à Poker complet | R♥ – D♠ | R♣ – D♦ – 5♠ | R♠ – R♦ – D♥ – D♣ | 4 |
| Une paire à Deux paires ou Mise | A♣ – D♦ | A♦ – 10♣ – 3♠ | A♥ – A♠ – D♥ – D♣ – D♠ | 5 |
| Pas de paire à une paire | 9♣ – 7♦ | 2♠ – 3♦ – V♣ | 9♠ – 9♥ – 9♦ – 7♣ – 7♥ – 7♠ | 6 |
| Deux cartes supérieure à Paire supérieure | A♦ – V♥ | 10♣ – 8♦ – 2♠ | A♣ – A♠ – A♥ – V♣ – V♦ – V♠ | 6 |
| Poker complet / Quatre d’entre eux | 6♣ – 6♦ | 6♠ – 7♥ – V♣ | 6♥ – 7♣ – 7♦ – 7♠ – V♦ – V♠ – V♥ | 7 |
| Tirage de Quinte illimité | 9♣ – 8♦ | 7♣ – 10♥ – 3♠ | A♦ – A♠ – A♥ – A♣ – 6♣ – 6♦ – 6♥ – 6♠ | 8 |
| Tirage de couleur | R♠ – V♠ | A♠ – 6♠ – 8♦ | 2♠ – 5♠ – 7♠ – 10♠ – D♠ | 9 |
| Quinte intérieur et deux cartes supérieure | A♣ – R♦ | D♥ – 10♣ – 2♠ | Vx – A♦ – A♥ – A♠ – R♥ – R♣ – R♠ | 10 |
| Tirage de quinte intérieur et couleur | A♦ – R♦ | V♦ – D♠ – 3♦ | 10x – 2♦ – 4♦ – 9♦ – D♦ | 12 |
| Quinte illimité et Tirage de couleur | R♥ – D♥ | 10♥ – V♠ – 4♥ | 9x – Ax – 2♥ – 3♥ – 5♥ – 8♥ – V♥ – | 15 |
Le décompte est un processus assez simple. Vous comptez simplement le nombre de cartes inconnues qui amélioreront votre main.
Après, il y a une ou deux choses dont vous devez tenir compte:
Ne comptez pas deux fois
Il y a 15 probabilités lorsque vous avez à la fois une quinte et un tirage de quinte.
Vous vous demandez peut-être pourquoi il y a 15 probabilités et non 17, puisqu’il y a 8 probabilités pour une quinte et 9 cotes pour une couleur (et 8 + 9 = 17).
La raison est, comme exemple dans notre exemple du tableau n°2, le A♥ et le 9♥ fera une couleur et complétera également une quinte.
Ces probabilités étant impossibles à compter deux fois, le total de nos probabilités pour ce type de tirage est de 15 et non 17.
Anti-cotes et bloqueurs
Il y a des probabilités qui amélioreront votre main mais qui ne vous aideront pas à gagner.
Par exemple, supposons que vous teniez 5♣ 4♦ dans un flop de 6♥ 3♠ D♥
Vous êtes sur une ligne droite et deux ou sept vous aideront à y arriver.
Cependant, le flop contient également deux cœurs, donc si vous touchez le 2♥ ou le 7♥ vous aurez une quinte, mais vous pourriez perdre contre une quinte de couleur.
Ainsi, sur 8 probabilités possibles, vous n’avez vraiment que 6 bonnes probabilités.
Il est généralement préférable de faire preuve de prudence dans l’évaluation de vos éventuelles probabilités.
Ne tombez pas dans le piège qui consiste à supposer que toutes vos probabilités vous aideront.
Certaines ne vous aideront pas, et il faut les exclure de l’équation.
Il y a les bons, les moins bons et les anti-cotes.
Gardez cela à l’esprit.
Calculer vos probabilités au poker
Une fois que vous savez combien de outs vous avez (n’oubliez pas de n’inclure que les “bons outs”), il est temps de calculer vos chances.
Il existe de nombreuses façons de calculer les chances réelles de réussir ces outs, et nous allons vous expliquer trois méthodes.
Cette première méthode ne nécessite pas de mathématiques, il suffit d’utiliser le tableau pratique ci-dessous :
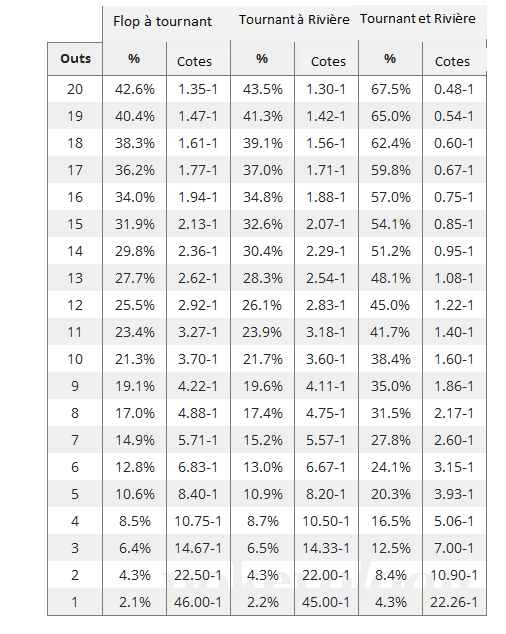
Comme vous pouvez le voir dans le tableau ci-dessus, si vous avez une couleur après le flop (9 outs) vous avez 19,1% de chances de la toucher au tour ou exprimé en cote, vous êtes à 4,22 contre 1.
Les probabilités sont légèrement meilleures du tournant à la rivière, et bien meilleures lorsque vous avez encore les deux cartes à venir.
En effet, au tour et à la rivière, vous avez 35 % de chances de tirer votre couleur, soit 1,86 contre 1.
Faire des calculs – Calculer les chiffres
Il y a plusieurs façons de faire le calcul. L’une est complète et totalement précise et l’autre, un raccourci qui est assez proche.
Prenons encore une fois un tirage au sort comme exemple. La probabilité de ne pas tirer la chasse d’eau du flop à la rivière est de 1,86 contre 1. Comment arriver à ce chiffre ? Voyons voir…
Avec 9 coeurs restants, il y aurait 36 combinaisons pour obtenir 2 coeurs et faire votre flush avec 5 coeurs.
Le calcul se fait comme suit :
(9 x 8 / 2 x 1) = (72 / 2) ≈ 36.
Il s’agit de la probabilité que deux coeurs courent alors que vous n’en avez besoin que d’un seul, mais il faut le calculer.
Sur les 47 cartes restantes inconnues, 38 peuvent se combiner avec n’importe lequel des 9 coeurs restants :
9 x 38 ≈ 342.
Nous savons maintenant qu’il y a 342 combinaisons de non cœur/coeur. Nous additionnons donc les deux combinaisons qui peuvent vous permettre de tirer la quinte flush :
36 + 342 ≈ 380.
Le nombre total de combos de tournants et de rivières est de 1081, calculé comme suit :
(47 x 46 / 2 x 1) = (2162 / 2) ≈ 1081.
Vous prenez maintenant les 380 façons possibles de faire et vous les divisez par le total des 1081 résultats possibles :
380 / 1081 = 35.18518%
Ce nombre peut être arrondi à 0,352 ou seulement à 0,35 en termes décimaux. Vous divisez 0,35 par sa réciproque de 0,65 :
0.65 / 0.35 = 1.8571428
Et voilà, c’est ainsi que nous atteignons 1,86. Si cela vous a donné le vertige, voici la méthode de la main courte car vous n’avez pas besoin de la connaître à 7 décimales.
La règle des quatre et deux
Une façon beaucoup plus simple de calculer les probabilités au poker est la méthode 4 et 2, qui consiste à multiplier vos outs par 4 lorsque vous avez à la fois le tour et la rivière à venir – et avec une carte à jouer (c’est-à-dire le tour à la rivière), vous multiplieriez vos outs par 2 au lieu de 4.
Imaginez qu’un joueur fasse tapis et qu’en suivant les instructions, vous soyez assuré de voir les cartes du tournant et de la rivière. Si vous avez neuf outs, alors il s’agit simplement d’un cas de 9 x 4 = 36. Cela ne correspond pas à la cote exacte indiquée dans le tableau, mais c’est assez précis.
Et avec une seule carte à venir ? C’est encore plus facile. Si l’on prend l’exemple de notre flush, neuf retraits équivaudraient à 18% (9 x 2).
Pour un tirage en quinte, il suffit de compter les retraits et de les multiplier par deux, ce qui donne 16 % (8 x 2) – soit près de 17 %. Là encore, c’est assez proche et facile à faire – il n’est pas nécessaire d’être un génie des mathématiques.
Et pour aller plus loin, trouver ici les meilleurs logiciels d’aide au poker
Les probabilités d’une certaine main de départ
| Main | Probabilité | Probabilités |
|---|---|---|
| A-Ks (ou toute autre carte spécifique adaptée) | 0.00302 | 331-1 |
| A-A (ou toute autre paire spécifique) | 0.00453 | 220-1 |
| A-Ks, K-Qs, Q-Js, or J-10s (cartes adaptées) | 0.0121 | 81.9-1 |
| A-K (ou toute autre paire spécifique, y compris celle qui convient) | 0.0121 | 81.9-1 |
| A-A, K-K, or Q-Q | 0.0136 | 72.7-1 |
| A-A, K-K, Q-Q, or J-J | 0.0181 | 54.3-1 |
| Cartes adaptées, valet ou mieux | 0.0181 | 54.3-1 |
| A-A, K-K, Q-Q, J-J, or 10-10 | 0.0226 | 43.2-1 |
| Cartes adaptées, 10 ou plus | 0.0302 | 32.2-1 |
| Connecteurs adaptés | 0.0392 | 24.5-1 |
| Cartes connectées, 10 ou plus | 0.0483 | 19.7-1 |
| Deux cartes de rang au moins égal à la dame | 0.0498 | 19.1-1 |
| N’importe quelle paire de poche | 0.0588 | 16-1 |
| Deux cartes de rang au moins égal au valet | 0.0905 | 10.1-1 |
| Deux cartes quelconques avec un rang d’au moins 10 | 0.143 | 5.98-1 |
| Cartes connectées (cartes de rang consécutif) | 0.157 | 5.38-1 |
| Deux cartes quelconques de rang au moins égal à 9 | 0.208 | 3.81-1 |
| Ni connectés ni adaptés, au moins un 2-9 | 0.534 | 0.873-1 |
Les probabilitésd’une main avec un certain nombre de outs
| Exemple de tirage au sort | Outs | Faire au tournant | Faire en rivière | Faire au tournant ou à la rivière | |||
|---|---|---|---|---|---|---|---|
| Prob. | probabilités | Prob. | probabilités | Prob. | probabilités | ||
| Quinte flush intérieure ; Quatre de la même sorte | 1 | 0.0213 | 46.0-1 | 0.0217 | 45.0-1 | 0.0426 | 22.5-1 |
| Quinte flush ouverte ; Trois de la même sorte | 2 | 0.0426 | 22.5-1 | 0.0435 | 22.0-1 | 0.0842 | 10.9-1 |
| Paire haute | 3 | 0.0638 | 14.7-1 | 0.0652 | 14.3-1 | 0.1249 | 7.01-1 |
| Quinte intérieur ; Full house | 4 | 0.0851 | 10.8-1 | 0.0870 | 10.5-1 | 0.1647 | 5.07-1 |
| Trois de la même sorte ou deux de la même paire | 5 | 0.1064 | 8.40-1 | 0.1087 | 8.20-1 | 0.2035 | 3.91-1 |
| L’une ou l’autre paire | 6 | 0.1277 | 6.83-1 | 0.1304 | 6.67-1 | 0.2414 | 3.14-1 |
| Full house ou quadruple ; Quinte intérieure ou paire haute | 7 | 0.1489 | 5.71-1 | 0.1522 | 5.57-1 | 0.2784 | 2.59-1 |
| Quinte ouverte | 8 | 0.1702 | 4.88-1 | 0.1739 | 4.75-1 | 0.3145 | 2.18-1 |
| Flush | 9 | 0.1915 | 4.22-1 | 0.1957 | 4.11-1 | 0.3497 | 1.86-1 |
| Quinte intérieure ou paire | 10 | 0.2128 | 3.70-1 | 0.2174 | 3.60-1 | 0.3839 | 1.60-1 |
| Paire ouverte, droite ou haute | 11 | 0.2340 | 3.27-1 | 0.2391 | 3.18-1 | 0.4172 | 1.40-1 |
| Inside straight or flush; Flush or high pair | 12 | 0.2553 | 2.92-1 | 0.2609 | 2.83-1 | 0.4496 | 1.22-1 |
| Paire ouverte, droite ou haute | 13 | 0.2766 | 2.62-1 | 0.2826 | 2.54-1 | 0.4810 | 1.08-1 |
| Quinte ou paire ouverte | 14 | 0.2979 | 2.36-1 | 0.3043 | 2.29-1 | 0.5116 | 0.955-1 |
| Quinte ouverte ou flush ; Flush ou paire ; Quinte intérieure, flush ou paire haute | 15 | 0.3191 | 2.13-1 | 0.3261 | 2.07-1 | 0.5412 | 0.848-1 |
| 16 | 0.3404 | 1.94-1 | 0.3478 | 1.88-1 | 0.5698 | 0.755-1 | |
| 17 | 0.3617 | 1.76-1 | 0.3696 | 1.71-1 | 0.5976 | 0.673-1 | |
| A l’intérieur : quinte, flush ou paire ; Quinte, flush ou paire ouverte | 18 | 0.3830 | 1.61-1 | 0.3913 | 1.56-1 | 0.6244 | 0.601-1 |
| 19 | 0.4043 | 1.47-1 | 0.4130 | 1.42-1 | 0.6503 | 0.538-1 | |
| 20 | 0.4255 | 1.35-1 | 0.4348 | 1.30-1 | 0.6753 | 0.481-1 | |
| Quinte ouverte, flush ou paire | 21 | 0.4468 | 1.24-1 | 0.4565 | 1.19-1 | 0.6994 | 0.430-1 |
| Main | Cotes | Pourcentage |
|---|---|---|
| Un flush | 118-1 | 0.8% |
| Une quinte en tenant deux cartes de connexion V-10 à 5-4 | 76-1 | 1.3% |
| Trois de la même sorte quand on tient une paire de poche | 7.5-1 | 11.8% |
| Une paire (correspondant à l’une de vos cartes) | 2.45-1 | 29.0% |
Les probabilités contre le flop
Cotes des deux mains l’une par rapport à l’autre en préflop (approximation)
| Situation | Mains | Probabilités | Pourcentage |
|---|---|---|---|
| Paire supérieure contre paire inférieure | Js Jc vs. 7h 7d | 4.09-1 | 80.3% vs. 19.7% |
| Paire contre deux cartes supérieures | 7s 7c vs. Ah Jd | 1.23-1 | 55.1% vs. 44.9% |
| Paire contre deux cartes inférieures | Qs Qc vs. 9h 7d | 4.77-1 | 82.7% vs. 17.3% |
| Paire contre une carte supérieure et une carte inférieure | Js Jc vs. Ah 7d | 2.50-1 | 71.4% vs. 28.6% |
| Deux cartes supérieures contre deux cartes inférieures | Qs Jc vs. 6h 5d | 1.70-1 | 62.9% vs. 37.1% |
| Une carte plus haute et une carte plus basse contre deux cartes du milieu | As 6c vs. Jh 9d | 1.27-1 | 55.9% vs. 44.1% |
| La plus haute et la troisième carte la plus élevée contre deuxième carte la plus élevée et la plus basse | As 6c vs. Jh 2d | 1.73-1 | 63.3% vs. 36.7% |
| Carte la plus élevée et commune contre carte la plus basse et commune | As Jc vs. Jh 9d | 2.74-1 | 73.3% vs. 26.7% |
Odds d’un overcard qui touche le tableau en tenant une paire de poche
| Main | Overcard dans leFlop | Overcard sur le tableau complet |
|---|---|---|
| 2-2 | 100% | 100% |
| 3-3 | 99.9% | 99.9997% |
| 4-4 | 99.4% | 99.988% |
| 5-5 | 98.1% | 99.91% |
| 6-6 | 95.8% | 99.6% |
| 7-7 | 92.1% | 98.8% |
| 8-8 | 86.7% | 96.9% |
| 9-9 | 79.3% | 93.3% |
| 10-10 | 69.5% | 86.9% |
| J-J | 57% | 76.3% |
| Q-Q | 41.4% | 59.9% |
| K-K | 22.6% | 35.3% |
| A-A | 0% | 0% |
Probabilité de faire face à une paire plus importante en tenant…
| Main | Contre 1 | Contre 2 | Contre 3 | Contre 4 | Contre 5 | Contre 6 | Contre 7 | Contre 8 | Contre 9 |
|---|---|---|---|---|---|---|---|---|---|
| K-K | 0.0049 | 0.0098 | 0.0147 | 0.0196 | 0.0244 | 0.0293 | 0.0342 | 0.0391 | 0.0439 |
| Q-Q | 0.0098 | 0.0195 | 0.0292 | 0.0388 | 0.0484 | 0.0579 | 0.0673 | 0.0766 | 0.0859 |
| J-J | 0.0147 | 0.0292 | 0.0436 | 0.0577 | 0.0717 | 0.0856 | 0.0992 | 0.1127 | 0.1259 |
| 10-10 | 0.0196 | 0.0389 | 0.0578 | 0.0764 | 0.0946 | 0.1124 | 0.1299 | 0.1470 | 0.1637 |
| 9-9 | 0.0245 | 0.0484 | 0.0718 | 0.0946 | 0.1168 | 0.1384 | 0.1593 | 0.1795 | 0.1990 |
| 8-8 | 0.0294 | 0.0580 | 0.0857 | 0.1125 | 0.1384 | 0.1634 | 0.1873 | 0.2101 | 0.2318 |
| 7-7 | 0.0343 | 0.0674 | 0.0994 | 0.1301 | 0.1595 | 0.1874 | 0.2138 | 0.2387 | 0.2619 |
| 6-6 | 0.0392 | 0.0769 | 0.1130 | 0.1473 | 0.1799 | 0.2104 | 0.2389 | 0.2651 | 0.2890 |
| 5-5 | 0.0441 | 0.0862 | 0.1263 | 0.1642 | 0.1996 | 0.2324 | 0.2623 | 0.2892 | 0.3129 |
| 4-4 | 0.0490 | 0.0956 | 0.1395 | 0.1806 | 0.2186 | 0.2532 | 0.2841 | 0.3109 | 0.3334 |
| 3-3 | 0.0539 | 0.1048 | 0.1526 | 0.1967 | 0.2370 | 0.2729 | 0.3040 | 0.3300 | 0.3503 |
| 2-2 | 0.0588 | 0.1141 | 0.1654 | 0.2124 | 0.2546 | 0.2914 | 0.3222 | 0.3464 | 0.3633 |
Probabilité de faire face à plusieurs grandes paires en tenant…
| Main | Contre 1 | Contre 2 | Contre 3 | Contre 4 | Contre 5 | Contre 6 | Contre 7 | Contre 9 |
|---|---|---|---|---|---|---|---|---|
| K-K | < 0.00001 | 0.00001 | 0.00003 | 0.00004 | 0.00007 | 0.00009 | 0.00012 | 0.00016 |
| Q-Q | 0.00006 | 0.00018 | 0.00037 | 0.00061 | 0.00091 | 0.00128 | 0.00171 | 0.00220 |
| J-J | 0.00017 | 0.00051 | 0.00102 | 0.00171 | 0.00257 | 0.00360 | 0.00482 | 0.00621 |
| 10-10 | 0.00033 | 0.00099 | 0.00200 | 0.00335 | 0.00504 | 0.00709 | 0.00950 | 0.01226 |
| 9-9 | 0.00054 | 0.00164 | 0.00330 | 0.00553 | 0.00836 | 0.01177 | 0.01580 | 0.02045 |
| 8-8 | 0.00081 | 0.00244 | 0.00493 | 0.00828 | 0.01253 | 0.01769 | 0.02378 | 0.03084 |
| 7-7 | 0.00112 | 0.00341 | 0.00689 | 0.01160 | 0.01758 | 0.02487 | 0.03351 | 0.04353 |
| 6-6 | 0.00149 | 0.00454 | 0.00918 | 0.01550 | 0.02353 | 0.03335 | 0.04503 | 0.05861 |
| 5-5 | 0.00191 | 0.00583 | 0.01182 | 0.01998 | 0.03040 | 0.04318 | 0.05840 | 0.07619 |
| 4-4 | 0.00239 | 0.00728 | 0.01480 | 0.02506 | 0.03821 | 0.05438 | 0.07371 | 0.09635 |
| 3-3 | 0.00291 | 0.00890 | 0.01812 | 0.03075 | 0.04698 | 0.06699 | 0.09099 | 0.11919 |
| 2-2 | 0.00349 | 0.01068 | 0.02180 | 0.03706 | 0.05673 | 0.08107 | 0.11034 | 0.14484 |
Probabilité de faire face à un as avec un plus grand joueur en tenant…
| Main | Contre 1 | Contre 2 | Contre 3 | Contre 4 | Contre 5 | Contre 6 | Contre 7 | Contre 8 | Contre 9 |
|---|---|---|---|---|---|---|---|---|---|
| AK | 0.00245 | 0.00489 | 0.00733 | 0.00976 | 0.01219 | 0.01460 | 0.01702 | 0.01942 | 0.02183 |
| AQ | 0.01224 | 0.02434 | 0.03629 | 0.04809 | 0.05974 | 0.07126 | 0.08263 | 0.09386 | 0.10496 |
| AJ | 0.02204 | 0.04360 | 0.06468 | 0.08529 | 0.10545 | 0.12517 | 0.14445 | 0.16331 | 0.18175 |
| AT | 0.03184 | 0.06266 | 0.09250 | 0.12139 | 0.14937 | 0.17645 | 0.20267 | 0.22805 | 0.25263 |
| A9 | 0.04163 | 0.08153 | 0.11977 | 0.15642 | 0.19154 | 0.22520 | 0.25745 | 0.28837 | 0.31799 |
| A8 | 0.05143 | 0.10021 | 0.14649 | 0.19038 | 0.23202 | 0.27152 | 0.30898 | 0.34452 | 0.37823 |
| A7 | 0.06122 | 0.11870 | 0.17266 | 0.22331 | 0.27086 | 0.31550 | 0.35741 | 0.39675 | 0.43369 |
| A6 | 0.07102 | 0.13700 | 0.19829 | 0.25523 | 0.30812 | 0.35726 | 0.40291 | 0.44531 | 0.48471 |
| A5 | 0.08082 | 0.15510 | 0.22338 | 0.28615 | 0.34384 | 0.39687 | 0.44561 | 0.49041 | 0.53160 |
| A4 | 0.09061 | 0.17301 | 0.24795 | 0.31609 | 0.37806 | 0.43442 | 0.48567 | 0.53227 | 0.57465 |
| A3 | 0.10041 | 0.19073 | 0.27199 | 0.34509 | 0.41085 | 0.47000 | 0.52322 | 0.57109 | 0.61416 |
| A2 | 0.11020 | 0.20826 | 0.29552 | 0.37315 | 0.44223 | 0.50370 | 0.55840 | 0.60706 | 0.65037 |
Un conseil d’administration composé de…
| Structure du tableau | Faire un flop | Faire un tournant | Faire une rivière | |||
|---|---|---|---|---|---|---|
| Prob. | Probabilités | Prob. | Probabilités | Prob. | Probabilités | |
| Trois ou plus de la même suite | 0.05177 | 18.3-1 | 0.13522 | 6.40-1 | 0.23589 | 3.24-1 |
| Quatre ou plus d’une même suite | 0.01056 | 93.7-1 | 0.03394 | 28.5-1 | ||
| Flop arc-en-ciel | 0.39765 | 1.51-1 | 0.10550 | 8.48-1 | ||
| Trois cartes de rang consécutif (mais pas quatre consécutives) | 0.03475 | 27.8-1 | 0.11820 | 7.46-1 | 0.25068 | 2.99-1 |
| Quatre cartes pour une quinte (mais pas cinq) | 0.03877 | 24.8-1 | 0.18991 | 4.27-1 | ||
| Trois cartes ou plus de rang consécutif et même suite | 0.00217 | 459-1 | 0.00869 | 114-1 | 0.02172 | 45.0-1 |
| Trois en un (mais pas un full house ou un quadruple) | 0.00235 | 424-1 | 0.00935 | 106-1 | 0.02128 | 46-1 |
| Une paire (mais pas deux paires ou trois ou quatre d’entre eux) | 0.16941 | 4.90-1 | 0.30417 | 2.29-1 | 0.42450 | 1.36-1 |
| Deux paires (mais pas un full) | 0.01037 | 95.4-1 | 0.04716 | 20.2-1 |
Qu’en pensez vous ?
Vous êtes libre de laisser un commentaire ci-dessous
Comment compte-t-on les mains de poker ?
Ce document vous permet de vous entraîner à compter, en utilisant des mains de poker comme test. Un jeu de poker standard comporte 52 cartes, chacune ayant un rang et une couleur. Les couleurs sont les symboles C = ♣, H = ♥, S = ♠, et D = ♦, et les rangs sont les symboles A, 2, 3, 4, 5, 6, 7, 8, 9, T = 10, J, Q, et K.
Quelle est la probabilité d'obtenir un full dans un jeu de 52 cartes ?
0.001441
Full house
Le nombre de ces mains est (13-choix-1)(4-choix-3)(12-choix-1)(4-choix-2). La probabilité est de 0,001441.
Comment compte-t-on les combinaisons de poker ?
Il est facile de calculer les combinaisons de mains au poker :
Les mains non appariées : Multipliez le nombre de cartes disponibles. (par exemple, AK sur un flop AT2 = [3 x 4] = 12 combinaisons AK).
Mains appariées : Trouvez le nombre de cartes disponibles. Retirez 1 de ce nombre, multipliez ces deux nombres ensemble et divisez par 2.
Comment lire les probabilités au poker ?
Les cotes du pot sont le rapport entre la taille du pot et la taille du pari. Par exemple, si le pot de départ est de 10 € et qu’un joueur parie 5 € – soit la moitié du pot – la taille du pot est alors de 15 € et un joueur fait face à une mise de 5 € La cote du pot est de 15:5 et, idéalement, vous voulez réduire le côté droit du ratio à un.


